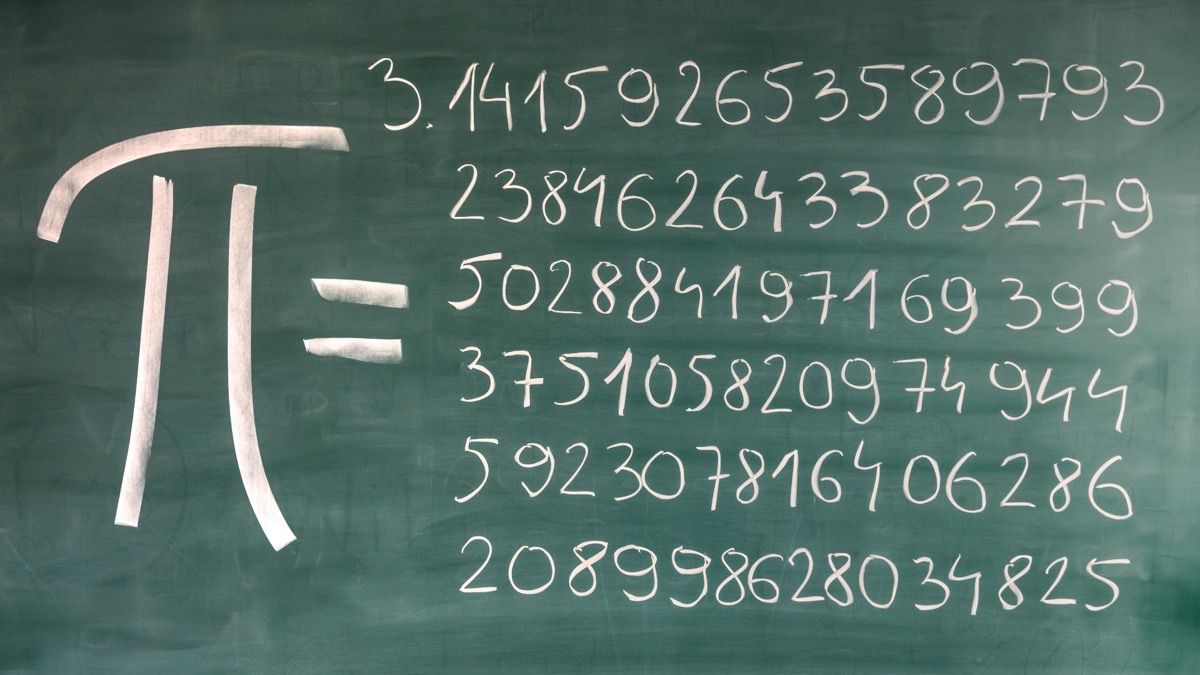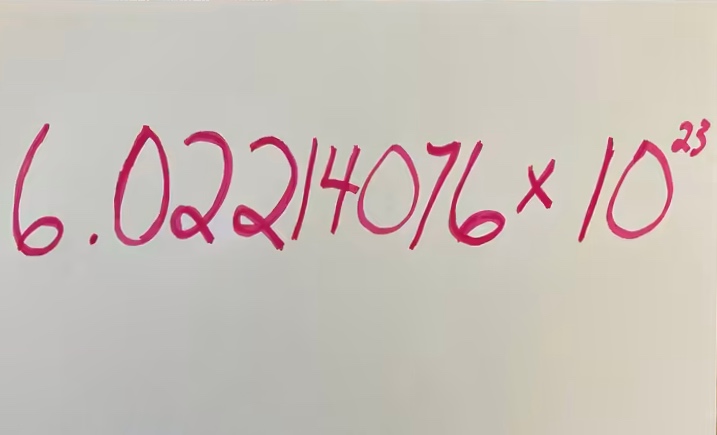- Pi (π): Bir dairenin çevresinin çapına oranı olarak bilinen ve yaklaşık olarak 3.14159 değerine sahip matematiksel bir sabittir.
- Euler Sayısı (e): Doğal logaritmanın tabanı olarak kullanılan ve yaklaşık olarak 2.71828 değerine sahip olan bir matematiksel sabittir.
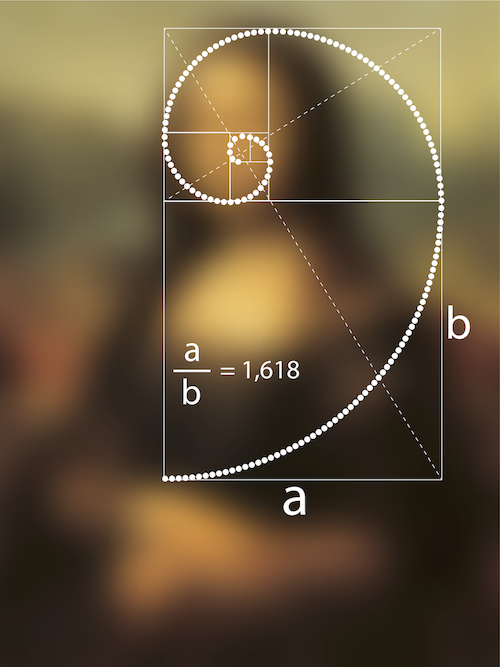
- Altın Oran (φ): Estetik ve matematiksel örüntülerde sıklıkla karşımıza çıkan ve yaklaşık olarak 1.61803 değerine sahip olan bir matematiksel sabittir.
- Avogadro Sayısı (Nₐ): Bir mol madde içindeki atom veya molekül sayısını temsil eden ve yaklaşık olarak 6.02214076 × 10^23 değerine sahip olan bir kimyasal sabittir.
- Boltzmann Sabiti (k): Termodinamik hesaplamalarda ve istatistiksel mekaniğin temelinde kullanılan ve yaklaşık olarak 1.380649 × 10^-23 J/K değerine sahip olan bir fiziksel sabittir.
- Işığın Hızı (c): Vakumda hareket eden ışığın hızını temsil eden ve yaklaşık olarak 299,792,458 m/s değerine sahip olan bir fiziksel sabittir.
- Plank Sabiti (h): Kuantum mekaniği hesaplamalarında kullanılan ve yaklaşık olarak 6.62607015 × 10^-34 J·s değerine sahip olan bir fiziksel sabittir.
- Ses Hızı (v_ses): Belirli bir ortamda ses dalgalarının yayılma hızını temsil eden ve standart koşullarda yaklaşık olarak 343 m/s değerine sahip olan bir fiziksel sabittir.
- Planck Zamanı (tₚ): Planck zamanı, Planck sabiti (h) ve ışık hızı (c) kullanılarak hesaplanan teorik bir zaman birimidir. Bu zaman birimi, 1.855 × 10^-43 saniyedir. Planck zamanı, kuantum mekaniği ve teorik fizikte önemli bir rol oynar.
- Gravitasyonel Sabit (G): Gravitasyonel sabit, iki kütle arasındaki kütleçekim kuvvetini hesaplamak için kullanılan bir fiziksel sabittir. Bu değer, yaklaşık olarak 6.67430 × 10^{-11} m³/kg s² şeklinde ifade edilir.
- Elektrik Sabiti (ε₀): Elektrik sabiti, elektrik alanın dielektrik bir ortamda yayılmasını açıklar. Bu değer, yaklaşık olarak 8.854 × 10^{-12} F/m (farad/metreye) eşittir.
- Manyetik Sabit (μ₀): Manyetik sabit, manyetik alanın bir ortam içinde yayılmasını açıklar. Bu değer, yaklaşık olarak 4π × 10^{-7} T m/A (tesla metre/amper) şeklinde ifade edilir.
- Elektron Kütlesi (mₑ): Elektron kütlesi, bir elektronun kütlesini temsil eder. Bu değer, yaklaşık olarak 9.109 × 10^{-31} kg şeklinde ifade edilir.
- Proton Kütlesi (mₚ): Proton kütlesi, bir protonun kütlesini temsil eder. Bu değer, yaklaşık olarak 1.673 × 10^{-27} kg şeklinde ifade edilir.
- Boltzmann Sabiti (k_B): Boltzmann sabiti, bir parçacığın kinetik enerjisi ve sıcaklık arasındaki ilişkiyi tanımlar. Bu değer, yaklaşık olarak 1.380649 × 10^{-23} J/K (jul/kelvin) şeklinde ifade edilir.
Bu sabitler, bilimsel hesaplamalardan sanata, mimariden astronomiye kadar geniş bir yelpazede önemli roller oynarlar. Bilim insanlarının ve mühendislerin matematik, fizik, kimya ve diğer bilim dallarında temel öneme sahip olan ve birçok farklı alanda kullanılan önemli sayılardır. Bilimsel hesaplamalar ve araştırmalar için vazgeçilmez ve farklı alanlarda matematiksel ve fiziksel ilişkilerin temelini oluşturan bu sayılar bilim insanlarının ve mühendislerin çalışmalarında ve keşiflerinde temel taşlarıdır.
Pi Sayısı
Pi Sayısı: Sonsuzluğun İfadesi Matematik dünyasının en ikonik ve gizemli sayılarından biri, hiç kuşkusuz, Pi sayısıdır (π). Pi, birçok matematiksel hesaplama ve geometrik problemin temel bir bileşeni olarak kabul edilir…
Avogadro Sayısı
Avogadro’nun sayısı, İtalyan kimyager Amedeo Avogadro tarafından ortaya konulmuştur. Avogadro, 1811 yılında yaptığı çalışmada gazların hacimleri ve molekülleri arasındaki ilişkiyi açıklarken, eşit hacimlerdeki gazlarda eşit sayıda molekül bulunması gerektiğini öne…
Fibonacci Dizisi
Fibonacci Dizisi: Matematiksel Özellikleri ve Uygulamaları Bu makalemde, Fibonacci dizisi olarak bilinen bir matematiksel dizinin özelliklerini ve çeşitli uygulamalarını inceleyeceğim. Fibonacci dizisi, her bir sayının kendisinden önce gelen iki sayının…
Altın Oran: Matematiksel ve Estetik Bir İnceleme
Altın oran, matematik ve sanat alanlarında uzun bir geçmişe sahip olan bir kavramdır. Doğada, sanatta ve hatta insan vücudunda gözlemlenebilen bir oran olarak büyük ilgi çekmiştir. Bu makalemde, altın oranın…
© 2023, Bedri Yılmaz.
BedriYilmaz.com by Bedri Yılmaz is licensed under Attribution-NonCommercial-NoDerivatives 4.0 International