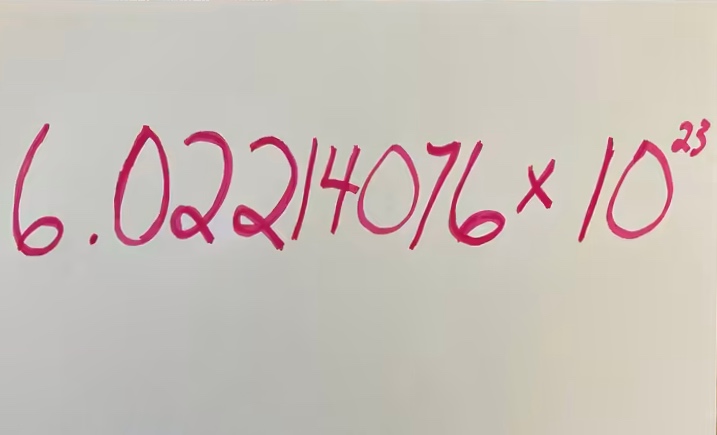Pi Sayısı: Sonsuzluğun İfadesi
Matematik dünyasının en ikonik ve gizemli sayılarından biri, hiç kuşkusuz, Pi sayısıdır (π). Pi, birçok matematiksel hesaplama ve geometrik problemin temel bir bileşeni olarak kabul edilir ve tarihsel olarak ilginç bir geçmişe sahiptir.
Pi’nin Tarihi Kökenleri
Pi’nin kökenleri, antik dünyaya dayanır. Mısırlılar ve Babilliler, yaklaşık değerlerle Pi’yi hesaplamışlardır. Ancak, Pi’nin modern anlamdaki kesirli ifadesi ve ondalık kesir gösterimi, Antik Yunan matematikçisi Archimedes’e atfedilir. M.Ö. 3. yüzyılda Archimedes, Pi’yi bir dairenin çevresinin çapına oranı olarak hesaplamıştır. Bu, Pi’nin geometrik bir anlamını ifade eden ilk hesaplamadır.
Pi Sayısının İrrasyonel Olduğu Keşfi
Pi’nin tam bir kesirli ifadeye sahip olup olmadığı uzun süre bir soru işaretiydi. Ancak, 1768 yılında Johann Lambert, Pi’nin irrasyonel (tam bir kesirli olmayan) bir sayı olduğunu matematiksel olarak kanıtladı. Bu, Pi’nin ondalık kesir gösteriminin sonsuz ve tekrar etmeyen bir desene sahip olduğu anlamına gelir. Yani, Pi’nin ondalık kesir gösterimi 3.14159265359… şeklinde sonsuza kadar devam eder, ancak herhangi bir tekrar eden desen yoktur.
Pi sayısının kesirli ifadesini bulmak için birçok matematikçi tarih boyunca çalışmıştır. Ancak Pi’nin irrasyonel (tam bir kesirli olmayan) bir sayı olduğunu ve ondalık kesir gösteriminin sonsuz ve tekrar etmeyen bir desene sahip olduğunu matematiksel olarak kanıtlayan ilk kişi, Johann Lambert’tir.
Johann Lambert, 1768 yılında Pi’nin irrasyonel olduğunu gösteren bir teorem geliştirdi. Bu teorem, Pi’nin tam bir kesirli ifadesinin olmadığını ve ondalık kesir gösteriminin sonsuza kadar devam ettiğini kanıtlamıştır. Bu önemli bir matematiksel keşiftir ve Pi’nin doğasını daha iyi anlamamıza yardımcı olmuştur.
Ancak Pi’nin yaklaşık değerini hesaplayan ilk matematikçiler Antik Yunan’dan itibaren gelir. Özellikle Archimedes M.Ö. 3. yüzyılda Pi’nin yaklaşık değerini hesaplamıştır. Onun dairenin çevresi ile çapı arasındaki ilişkiyi kullanarak Pi’yi yaklaşık olarak 3.14 olarak hesapladığı bilinmektedir. Bu da Pi’nin kesirli bir ifadesinin olmadığını ve yaklaşık değerinin antik çağlarda bile bilindiğini gösterir.
Pi’nin Hesaplanması
Pi sayısını hesaplamak için birçok farklı yöntem bulunmaktadır. Bunlardan en basitleri, dairelerin çevresi ile çapı arasındaki ilişkiyi kullanmaktadır. Örneğin, Archimedes’in yöntemi Pi’yi hesaplamak için bir yöntemdir. Bunun yanı sıra, Pi sayısını hesaplamak için bilgisayarlar kullanarak yapılan sayısal yaklaşımlar da vardır. Bu yöntemler, Pi’nin ondalık kesir gösterimini daha fazla basamakla hesaplamanıza olanak tanır.
İlginç Pi Sayısı Gerçekleri
- Pi, matematikteki en tanınmış irrasyonel sayılardan biridir.
- Bilgisayarlar sayesinde Pi’nin ondalık kesir gösterimi milyonlarca basamağa kadar hesaplanmıştır.
- Pi sayısının bilgisayarların matematiksel hesaplamaları için önemli bir rolü vardır, özellikle trigonometri ve geometri alanlarında.
- Pi’nin ondalık kesir gösterimi, birçok bilim ve mühendislik uygulamasında kullanılır.
Sonuç olarak, Pi sayısı matematiğin temel taşlarından biridir ve tarihsel olarak ilginç bir geçmişe sahiptir. Bu irrasyonel sayı, matematiksel hesaplamaların ve geometrinin vazgeçilmez bir parçasıdır ve sayısız matematikçi ve bilim insanı tarafından incelenmiştir. Pi’nin tam değerini hesaplamak için çeşitli yöntemler bulunsa da, onun sonsuzluğunu ve gizemini çözmek hala matematiğin büyüleyici bir sorusu olarak durmaktadır.
Pi Sayısının Virgülden Sonraki İlk 250 Rakamı:
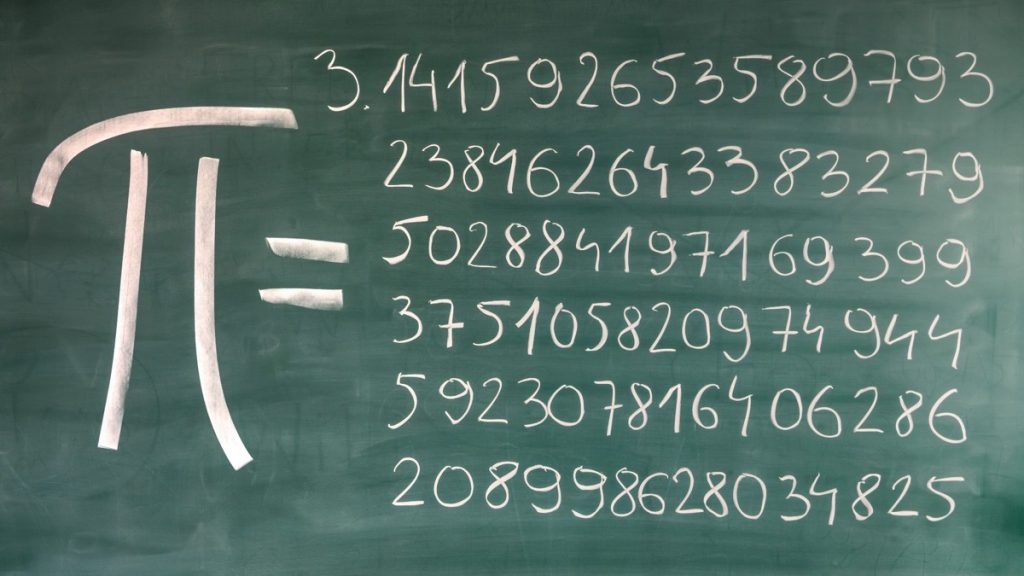
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912983367336244065664308602139494639522473719070217986094370277053921717629317675238467481846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892307852257066338622235369317931800607667263505505600695917073430306701554920293460908784439658253375438856909411303150952617937800297412076651479394259029896959469955657612186561967337862362561252163208628692221032748892186543648022967807057656151446320469279068212073883778142335628236089632080682224680122482611771858963814091839036736722208883215137556003727983940041529700287830766709444745601345564172543709069793961225714298946715435784687886144458123145935719849225284716050492212424701412147805734551050080190879927244284909188845801561660979191338754992005240636899125607176060588611646710940507754100225698315520005593572972571636269561882670428252483600823257530420752963450
Bu rakamlar Pi sayısının virgülden sonraki ilk 250 hanesidir. Pi, irrasyonel bir sayı olduğu için ondalık kesir gösterimi sonsuza kadar devam eder ve herhangi bir tekrar eden desen içermez. Bu nedenle Pi’nin daha fazla rakamı hesaplandıkça, ondalık kesir gösterimi daha fazla hassasiyet kazanır.
[wp_show_posts id=”9561″]
