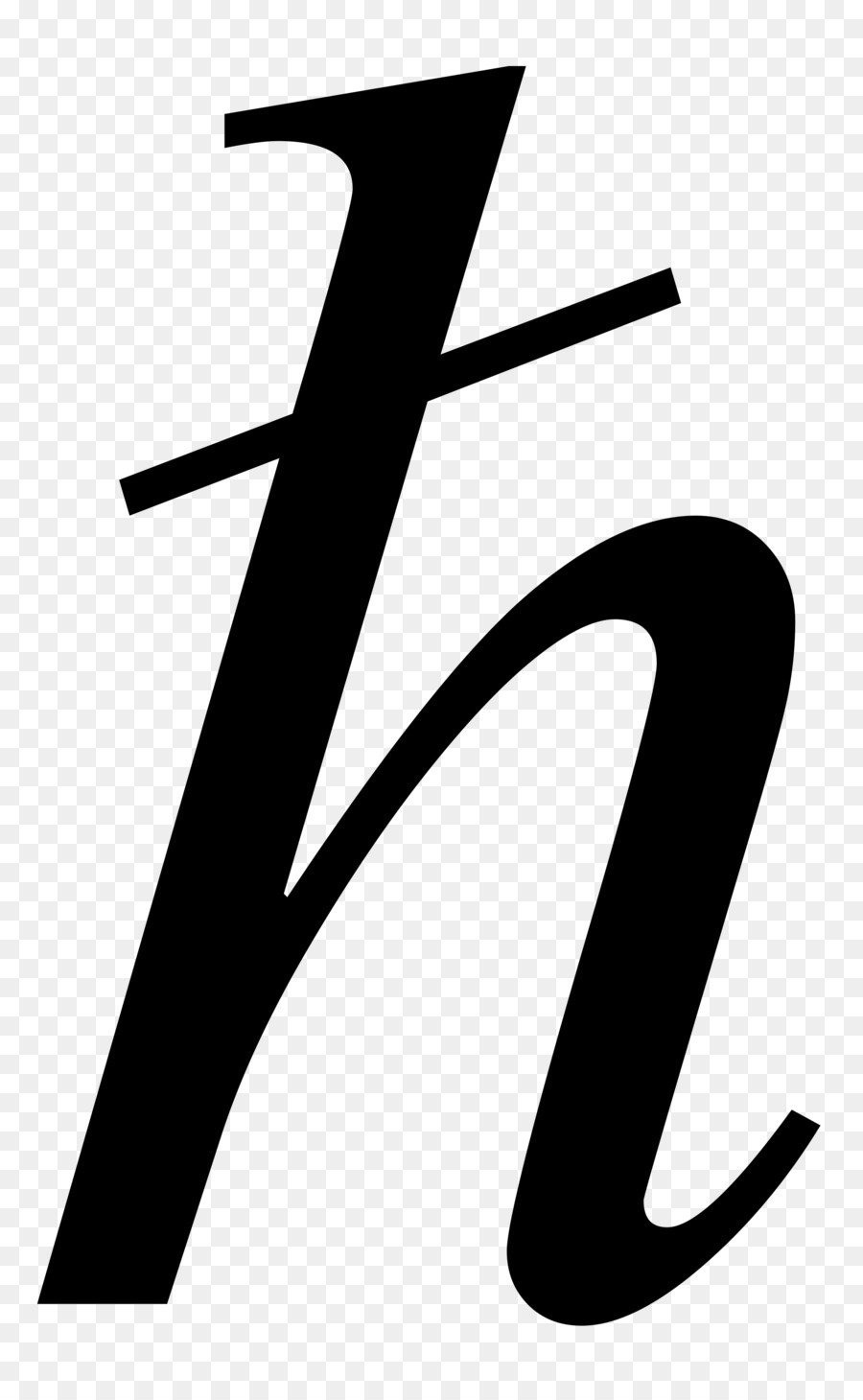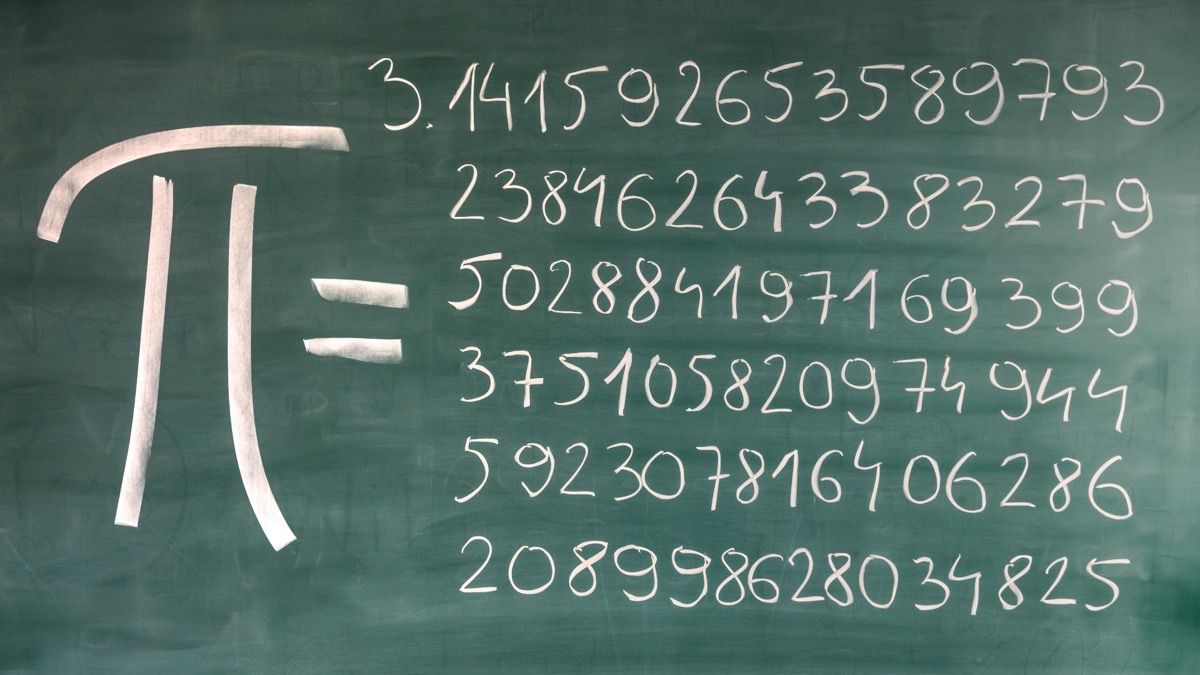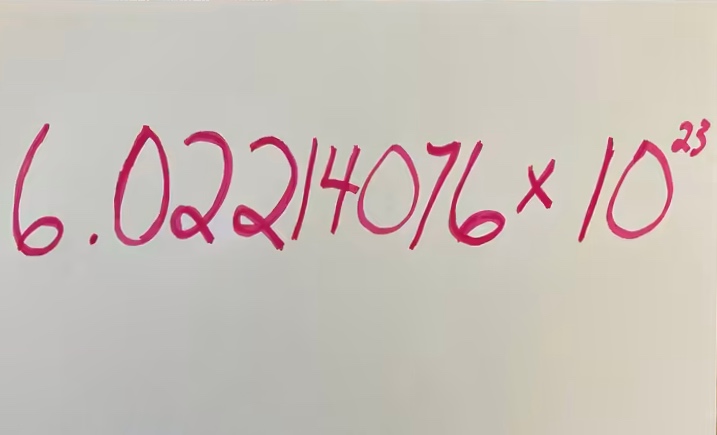Altın oran, matematik ve sanat alanlarında uzun bir geçmişe sahip olan bir kavramdır. Doğada, sanatta ve hatta insan vücudunda gözlemlenebilen bir oran olarak büyük ilgi çekmiştir. Bu makalemde, altın oranın matematiksel özellikleri, tarihçesi ve estetik değerini inceleyeceğim.
1. Altın Oranın Matematiksel Tanımı
Altın oran, iki farklı uzunluk arasındaki oranın, daha büyük olan uzunluğun, daha küçük olan uzunluğa olan oranıyla eşit olduğu bir orandır. Bu oran, genellikle φ (phi) sembolüyle temsil edilir ve yaklaşık olarak 1.61803 olarak ifade edilir. Matematiksel olarak, aşağıdaki denklemle ifade edilir:
φ = (1 + √5) / 2 ≈ 1.61803
Bu tanım, altın oranın temel matematiksel özelliğini ifade etmektedir.
2. Altın Oranın Tarihçesi
Altın oran, antik çağlardan beri matematiksel ve sanatsal çalışmalarda yer almıştır. İlk olarak Antik Yunan döneminde kullanılmış ve keşfedilmiştir. Ünlü matematikçi ve filozof Pisagor, altın oranın matematiksel özelliklerini ve estetik değerini incelenmiştir. Pisagorcular, altın oranın doğada ve evrende yaygın olarak bulunduğuna inanmışlardır.
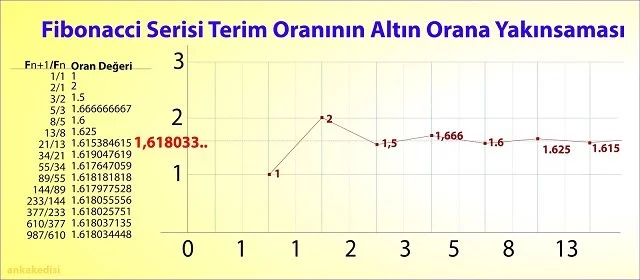
Altın oran, aynı zamanda Ortaçağ’da matematiksel çalışmalara ilham vermiştir. Leonardo Fibonacci’nin sayı dizisi, altın oranın ilginç bir özelliğini sergiler. Fibonacci dizisinde her sayı, kendisinden önceki iki sayının toplamı olarak bulunur. Bu dizideki ardışık sayıların birbirine oranı, Fibonacci oranları olarak bilinir ve yaklaşık olarak altın orana yaklaşır.
3. Altın Oranın Estetik Değeri
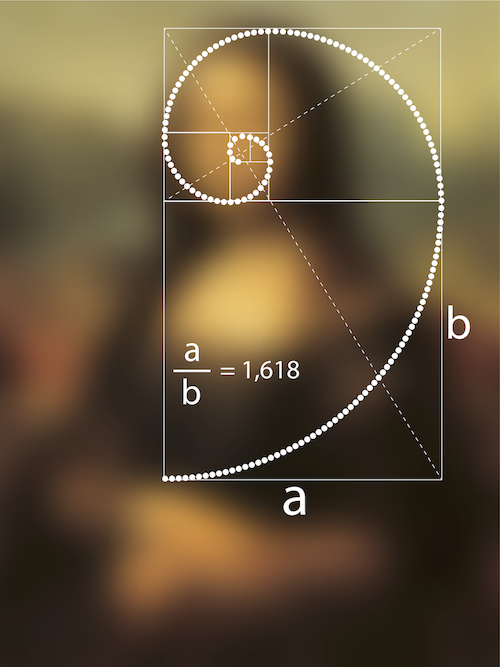
Altın oranın estetik değeri, sanat ve mimarlık alanlarında uzun bir süredir tartışılan bir konudur. Birçok sanatçı, yapıtlarında altın oranı kullanarak estetik açıdan hoş bir denge ve uyum elde etmeye çalışmıştır. Altın oranın önerdiği oranlar, insan gözüne hoş gelen ve estetik olarak algılanan bir düzen sunar.
Örneğin, ünlü İtalyan ressam Leonardo da Vinci’nin Mona Lisa tablosunda altın oranın bazı özelliklerinin kullanıldığı düşünülmektedir. Tablonun çerçeve boyutları ve figürün konumu, altın oranın prensiplerine uygun olabilecek şekilde düzenlenmiştir. Bu tür estetik tercihler, altın oranın sanatsal değerini vurgulamaktadır.
4. Altın Oranın Doğada Gözlemlenmesi
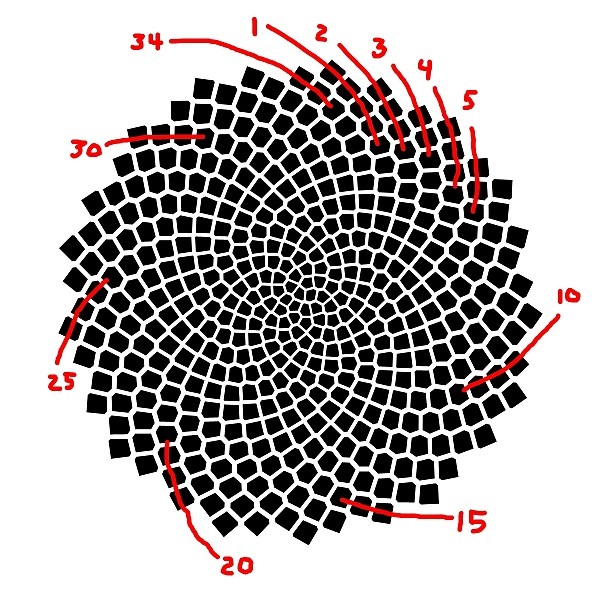
Altın oran, doğada da birçok örnekte gözlemlenebilir. Bitkilerin yaprak düzenleri, çiçeklerin spiral desenleri ve deniz kabuklarının yapısı gibi birçok doğal oluşumda altın orana rastlanır. Bu, altın oranın evrende yaygın bir matematiksel ve estetik prensip olduğunu göstermektedir.
Örneğin, ay çiçeği başta olmak üzere birçok bitkinin yapraklarının düzeni altın oranı takip eder. Bir yaprağın boyu, diğer yaprağın boyuna olan oran, altın oran değerine yaklaşır. Ayrıca, birçok deniz kabuğunun spiral yapısı, altın oranın matematiksel özelliklerini sergiler.
Altın oran, matematiksel ve estetik bir kavram olarak uzun bir geçmişe sahiptir. Matematiksel olarak, iki uzunluk arasındaki oranın altın oran olduğu söylenir. Altın oran, antik çağlardan beri matematikçiler, filozoflar, sanatçılar ve mimarlar tarafından ilgi çekici bir konu olarak ele alınmıştır. Doğada ve sanatta gözlemlenen birçok örnek, altın oranın evrensel bir prensip olduğunu göstermektedir. Altın oran, matematiksel ve estetik açıdan incelenmeye devam eden bir konu olmaya devam etmektedir.
Kaynaklar
- Livio, M. (2003). The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. Broadway Books.
- Huntley, H. E. (1970). The Divine Proportion: A Study in Mathematical Beauty. Dover Publications.
- Schwaller, L. (2017). Nature’s Harmonic Unity: A Treatise on Its Relation to Proportional Form. Inner Traditions.
- Matila, M. (2015). The Golden Ratio: The Divine Beauty of Mathematics. Race Point Publishing.
Bilimde Kullanılan 15 Önemli Sabit Sayı
Pi (π): Bir dairenin çevresinin çapına oranı olarak bilinen ve yaklaşık olarak 3.14159 değerine sahip matematiksel bir sabittir. Euler Sayısı (e): Doğal logaritmanın tabanı olarak kullanılan ve yaklaşık olarak 2.71828…
Pi Sayısı
Pi Sayısı: Sonsuzluğun İfadesi Matematik dünyasının en ikonik ve gizemli sayılarından biri, hiç kuşkusuz, Pi sayısıdır (π). Pi, birçok matematiksel hesaplama ve geometrik problemin temel bir bileşeni olarak kabul edilir…
Avogadro Sayısı
Avogadro’nun sayısı, İtalyan kimyager Amedeo Avogadro tarafından ortaya konulmuştur. Avogadro, 1811 yılında yaptığı çalışmada gazların hacimleri ve molekülleri arasındaki ilişkiyi açıklarken, eşit hacimlerdeki gazlarda eşit sayıda molekül bulunması gerektiğini öne…
Fibonacci Dizisi
Fibonacci Dizisi: Matematiksel Özellikleri ve Uygulamaları Bu makalemde, Fibonacci dizisi olarak bilinen bir matematiksel dizinin özelliklerini ve çeşitli uygulamalarını inceleyeceğim. Fibonacci dizisi, her bir sayının kendisinden önce gelen iki sayının…
© 2023, Bedri Yılmaz.
BedriYilmaz.com by Bedri Yılmaz is licensed under Attribution-NonCommercial-NoDerivatives 4.0 International
