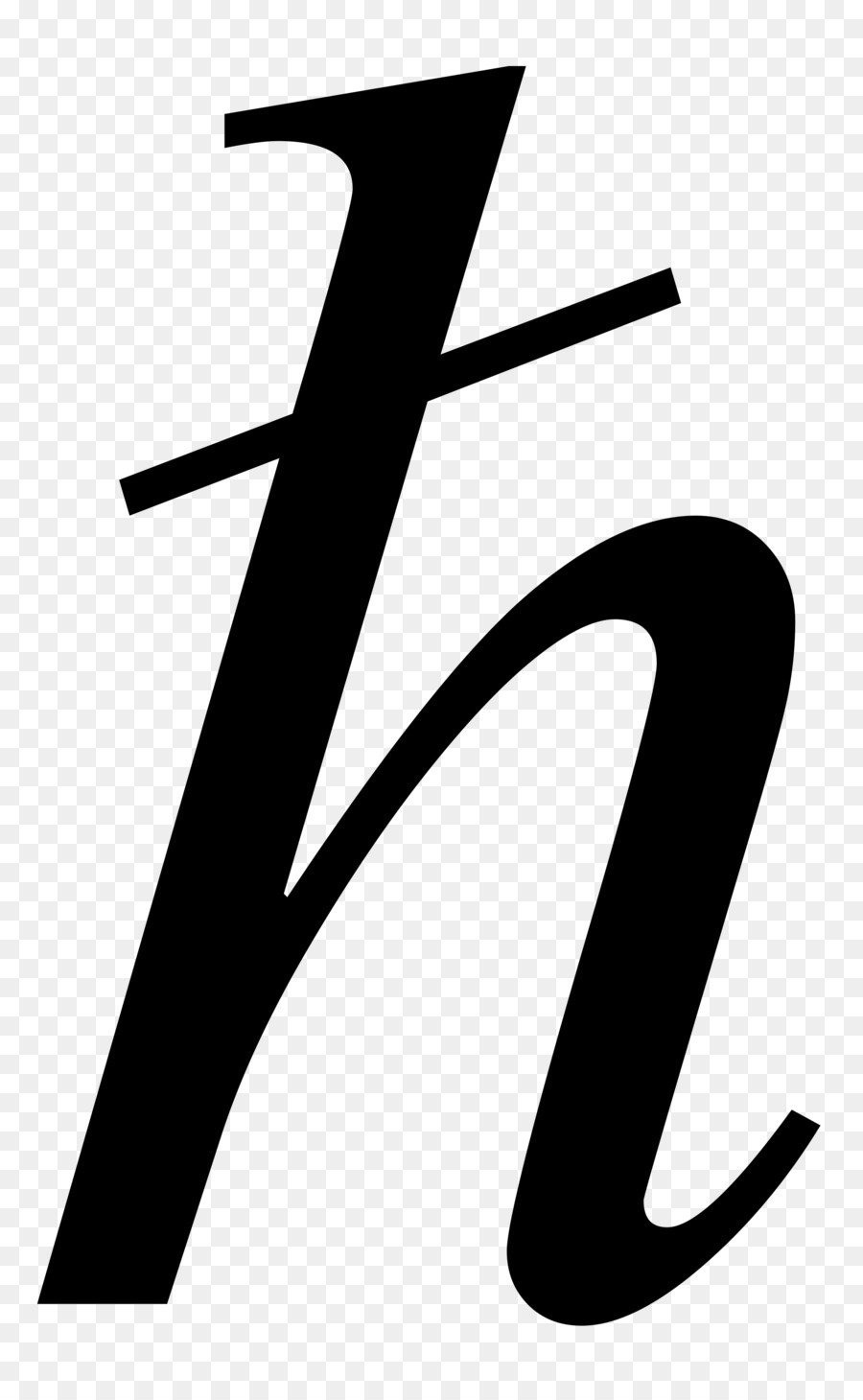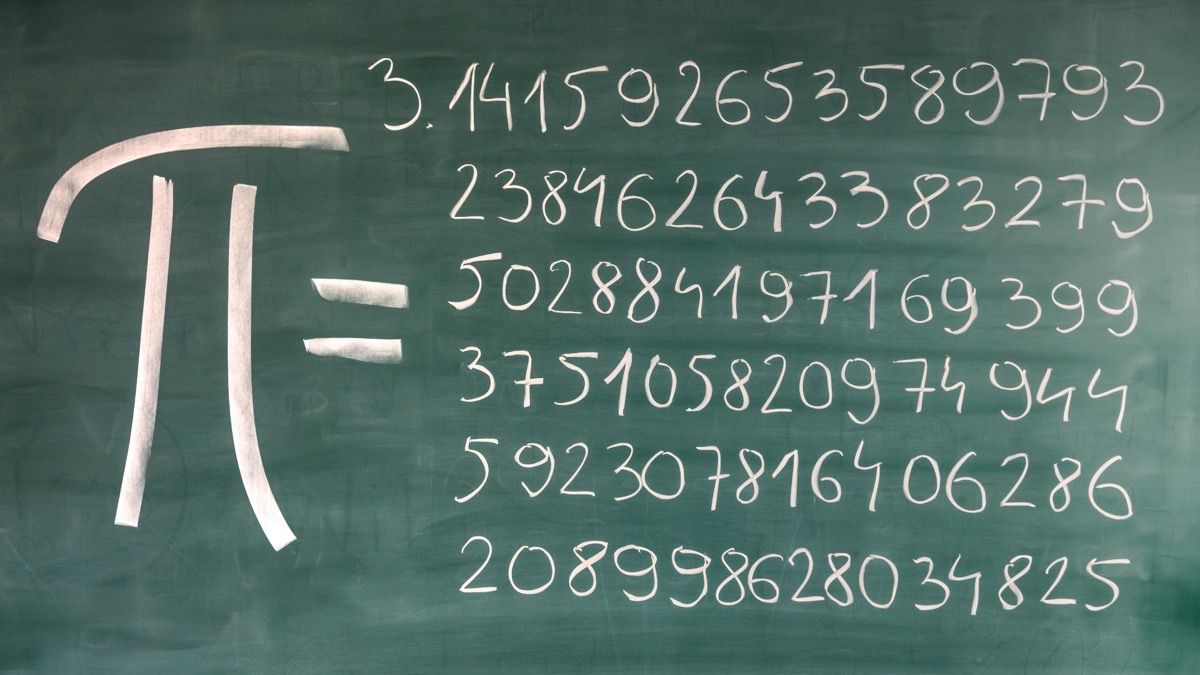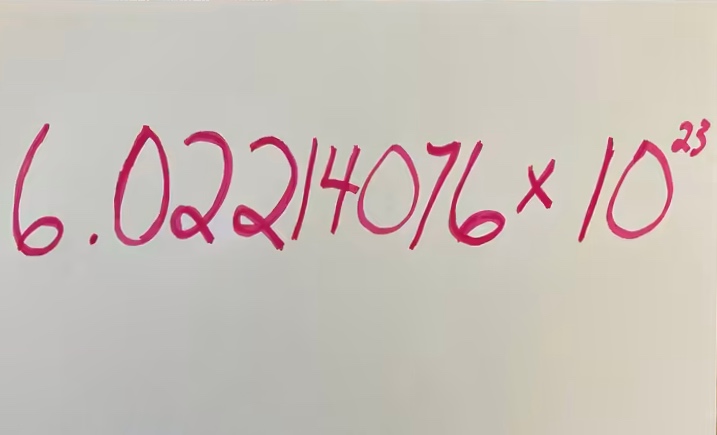Fibonacci Dizisi: Matematiksel Özellikleri ve Uygulamaları
Bu makalemde, Fibonacci dizisi olarak bilinen bir matematiksel dizinin özelliklerini ve çeşitli uygulamalarını inceleyeceğim. Fibonacci dizisi, her bir sayının kendisinden önce gelen iki sayının toplamıyla elde edildiği bir sayı dizisidir. Dizinin başlangıcı genellikle 0 ve 1’dir, yani 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, gibi devam eder. Fibonacci dizisi, antik çağlardan beri matematikçiler, bilim insanları ve sanatçılar arasında büyük ilgi görmüştür.
Fibonacci dizisi, İtalyan matematikçi Leonardo Fibonacci’nin 13. yüzyılda ortaya attığı bir kavramdır. Ancak bu dizi, antik Hint matematikçilerin çalışmalarında da izlerine rastlanmaktadır. Fibonacci dizisi, doğada, geometride, finansal analizde ve bilgisayar biliminde birçok ilgi çekici özelliği olan bir fenomen olarak görülmektedir.
Matematiksel Özellikler
Fibonacci dizisi, matematiksel olarak birçok ilginç özelliğe sahiptir. Örneğin:
- Dizi sonsuzdur: Fibonacci dizisi sonsuz bir dizidir ve herhangi bir sınıra veya sona erme noktasına sahip değildir.
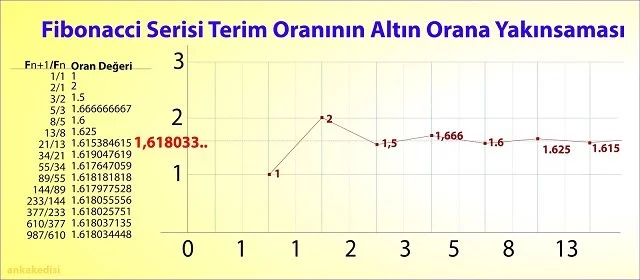
- Altın oran ilişkisi: Fibonacci dizisindeki ardışık terimler birbirine oranlandığında yaklaşık olarak 1.618 (altın oran) değerini yakalar. Bu altın oran, sanat, mimari ve doğada görülen birçok yapıda estetik bir denge unsuru olarak kabul edilir.
- İlişkili matematiksel kavramlar: Fibonacci dizisi, kombinatorik, kümeler teorisi, binom açılımı ve diğer matematiksel kavramlarla ilişkilidir. Örneğin, Fibonacci dizisi, Pascal üçgenindeki sayılarla ilişkilendirilebilir.
Uygulamalar
Fibonacci dizisi, birçok alanda uygulamalara sahiptir. Aşağıda bazı önemli uygulama alanlarından örnekler verilmiştir:
- Doğa bilimleri: Fibonacci dizisi, bitkilerin büyüme paternlerinde ve yaprak düzenlerinde görülebilir. Örneğin, ayçiçeği başaklarındaki tohumların düzeni, bir Fibonacci spirali şeklinde oluşur.
- Finansal analiz: Fibonacci dizisi, finansal piyasalarda trend analizi ve fiyat tahmininde kullanılır. Teknik analizde Fibonacci geri çekilme seviyeleri ve uzantıları önemli araçlardır.
- Bilgisayar bilimi: Fibonacci dizisi, algoritmalar, veri yapıları ve optimizasyon problemleri gibi birçok bilgisayar bilimi konusunda kullanılabilir. Örneğin, Fibonacci sayıları, bazı sıralama algoritmalarında performans analizi için bir metrik olarak kullanılır.
Fibonacci dizisi, matematiksel olarak ilginç ve çeşitli uygulamalara sahip olan bir sayı dizisidir. Doğada, sanatta, finansal analizde ve bilgisayar biliminde birçok alanda gözlemlenen Fibonacci desenleri, doğal dünyanın matematiksel temellerini anlamamıza yardımcı olur. Fibonacci dizisinin matematiksel özelliklerini daha iyi anlamak, gelecekteki araştırmalara ve uygulamalara ilham verebilir.
Kaynaklar
- Vajda, S. (2008). Fibonacci and Lucas Numbers, and the Golden Section: Theory and Applications. Dover Publications.
- Knott, R. (2003). The Fibonacci Numbers and Golden section in Nature. Mathematics Department, University of Surrey.
- Eswaran, K., \& Antoniou, I. (2016). Fibonacci Sequence and Its Applications. IUP Journal of Applied Mathematics, 12(2), 7-18.
Bilimde Kullanılan 15 Önemli Sabit Sayı
Pi (π): Bir dairenin çevresinin çapına oranı olarak bilinen ve yaklaşık olarak 3.14159 değerine sahip matematiksel bir sabittir. Euler Sayısı (e): Doğal logaritmanın tabanı olarak kullanılan ve yaklaşık olarak 2.71828…
Pi Sayısı
Pi Sayısı: Sonsuzluğun İfadesi Matematik dünyasının en ikonik ve gizemli sayılarından biri, hiç kuşkusuz, Pi sayısıdır (π). Pi, birçok matematiksel hesaplama ve geometrik problemin temel bir bileşeni olarak kabul edilir…
Avogadro Sayısı
Avogadro’nun sayısı, İtalyan kimyager Amedeo Avogadro tarafından ortaya konulmuştur. Avogadro, 1811 yılında yaptığı çalışmada gazların hacimleri ve molekülleri arasındaki ilişkiyi açıklarken, eşit hacimlerdeki gazlarda eşit sayıda molekül bulunması gerektiğini öne…
Altın Oran: Matematiksel ve Estetik Bir İnceleme
Altın oran, matematik ve sanat alanlarında uzun bir geçmişe sahip olan bir kavramdır. Doğada, sanatta ve hatta insan vücudunda gözlemlenebilen bir oran olarak büyük ilgi çekmiştir. Bu makalemde, altın oranın…
© 2023, Bedri Yılmaz.
BedriYilmaz.com by Bedri Yılmaz is licensed under Attribution-NonCommercial-NoDerivatives 4.0 International
